0×01 引言
为什么会想到这个呢?上周末做了“强网杯”的童鞋们应该都能知道吧,它其中有个密码学的题目就是考的这一点。
0×02 sha1的hash原理
说到要解释sha1的原理其实是非常复杂的,反正我这种智商的暂时还无法理解。所以,只能从面上跟大家谈一下我的理解。

首先,当hash函数拿到需要被hash的字符串后,先将其字节长度整除64,取得余数。如果该余数正好等于56,那么就在该字符串最后添加上8个字节的长度描述符(具体用bit表示)。如果不等于56,就先对字符串进行长度填充,填充时第一个字节为hex(80),其他字节均用hex(00)填充,填充至余数为56后,同样增加8个字节的长度描述符(该长度描述符为需要被hash的字符串的长度,不是填充之后整个字符串的长度)。以上过程,称之为补位。
补位完成后,字符串以64位一组进行分组(因为上面的余数为56,加上8个字节的长度描述符后,正好是64位,凑成一组)。字符串能被分成几组就会进行多少次“复杂的数学变化”。每次进行“复杂的数学变化”都会生成一组新的registers值供下一次“复杂的数学变化”来调用。第一次“复杂的数学变化”会调用程序中的默认值。当后面已经没有分组可以进行数学变化时,该组生成的registers值就是最后的hash值。
在sha1的运算过程中,为确保同一个字符串的sha1值唯一,所以需要保证第一次registers的值也唯一。所以在sha1算法中,registers具有初始值。如上图中的registers值0。
Hash值的随机性完全依赖于进行“复杂的数学变化”时输入的registers值和该次运算中字符串分组的数据。如果进行“复杂数学变化”时输入的registers值和该次运算的字符串分组相同,那么他们各自生成的新的registers值也相同。
0×03 举个栗子
当需要被hash的字符串为str_a = ”123456”,程序首先判断,len(str_a) % 64 == 56是否成立。这里很明显不成立。那么程序就进行补位操作。首先补位成余数为56的长度。

如上图,蓝色字体就为程序对该字符串进行补位的数据。当满足len(str_a) % 64 == 56后,程序就在该字符串的后面添加8个字节的长度描述符。注意,此处的长度为原始需要被hash的长度。也就是len(str_a) = 6字节*8bit/字节= 48bit=0x30bit。

补位+长度描述符=64个字节,正好是一个分组。所以此处只要进行一次复杂的数学变化就可以了。程序根据该64个字节的数据和registers值0生成新的registers值1。那么该新的registers值1就是str_a的sha1值
0×04 如何利用?
讲了这么多,好像都没讲到如何利用该扩展攻击。那么下面,重点来了。
我们还是利用这篇文章上面的例子进行讲解,转到FreeBuf之前文章。
简单来说,就是服务器上会生成一个salt值,该salt值你是不可预测的。但是你又知道了sha1(salt+filename)的值,该filename的值你也是知道的。假设此处的filename的值report.pdf,最后sha1的值为:0a8d538b724c6f2b4288526eb540ee7c。为了方便理解,我们继续假设salt的长度为16位。

将上图的字符串进行sha1操作时,同样先进行整除,然后取余。最后再补上8位的长度描述符。补位+添加长度描述符后的字符串如下图:
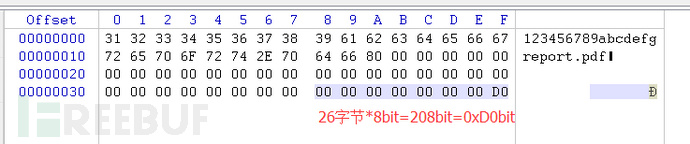
该长度也就满足了64位的分组,只需要进行一次“复杂的数学运算”就可以得到最后的sha1值了。
下面请各位看官思考如何进行下面一个字符串的sha1操作。

同样,还是先进行分组。由于该字符串的长度大于64个字节,且小于128个字节,所以要分成两组,需要进行两次“复杂的数学运算”。这个时候我们发现,第一个分组的数据和上图中补码后的数据完全一样,又因为他们都是第一个分组,初始的registers值也一样。那么经过第一轮“复杂的数学运算”,他们各自生成的registers值也同样是相同的。唯一不同的是,由于上面的长度小于64字节,所以只需要进行一轮运算便得到了最后的sha1值。然后这里的字符串有两个分组,需要将第一轮更新的registers值(也就是第一轮运算出来的sha1值)作为第二轮“复杂的数学运算”的registers值,然后才能得出最终的sha1值。
根据上面例子就说明,如果salt的值你不知道,但是你知道长度,又知道sha1(salt),那么就也就可以知道sha1(salt+“填充数据”+“任意可控数据”).这里的salt+“填充数据”就是对salt进行sha1时所补全的数据+最后8位的长度描述符。一般来说,salt+”填充数据”的长度就是64字节,正好是一个分组。如果salt的长度就大于了56个字节,那么加入填充数据后的长度应该是N个64字节,等于N个分组。
为什么?你可以想象,sha1程序再对(salt+“填充数据”+“任意可控数据”)进行hash时,只需要进行第二轮及第二轮以后的运算。因为第一轮运算后的registers值就是sha1(salt)的值,该值你已经知道了。
什么??还是不懂??你把上面的例子中的“123456789abcdefgreport.pdf”想成是salt,然后再考虑下呢?
如果有想更深入理解该原理的童鞋,可以拜读刺总的《白帽子讲web安全》中的“Understanding MD5 Length Extension Attack”一节。
*作者:二维码,本文属FreeBuf原创奖励计划,未经许可禁止转载
